Chapter 11: Generalized Linear Models for Count Data

Contents

11.1. Components of generalized linear models

11.2. GLMs for count data

11.3. Models for overdispersed count data

11.4. Models for excess zero counts

11.5. Case studies

11.6. Diagnostic plots for model checking

11.7. Multivariate response GLM models^*

11.8. Chapter summary

11.9. Lab exercises

Selected figures

• 

  Figure 11.2

  Exploratory plots for the number of articles in the PhdPubs data. Left: boxplots for married (1) vs. non-married (0); right: jittered scatterplot vs. mentor publications with a lowess smoothed curve.
• 

  Figure 11.3

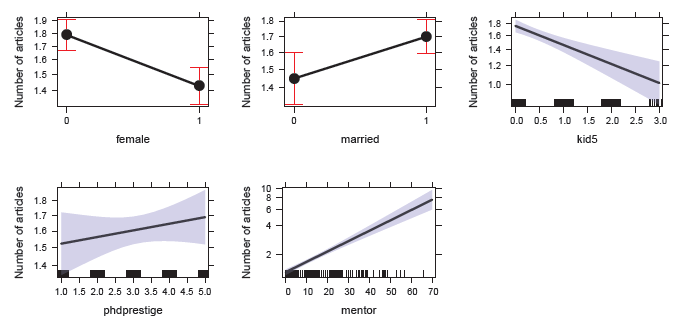
  Effect plots for the predictors in the Poisson regression model for the PhdPubs data. Jittered values of the continuous predictors are shown at the bottom as rug-plots.
• 

  Figure 11.4

  Generalized pairs plot for the CrabSatellites data.
• 

  Figure 11.7

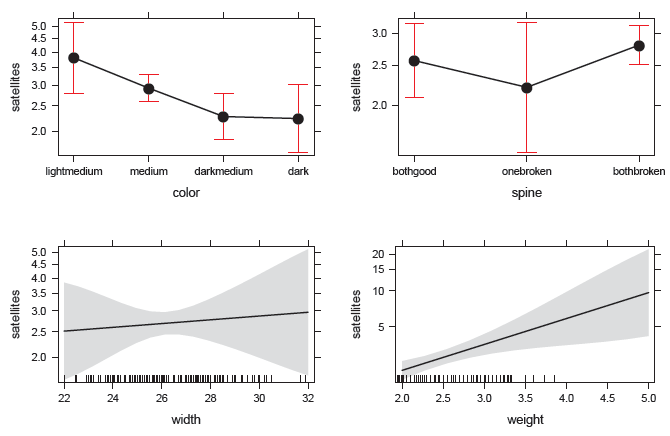
  Effect plots for the predictors in the Poisson regression model for the CrabSatellites data.
• 

  Figure 11.8

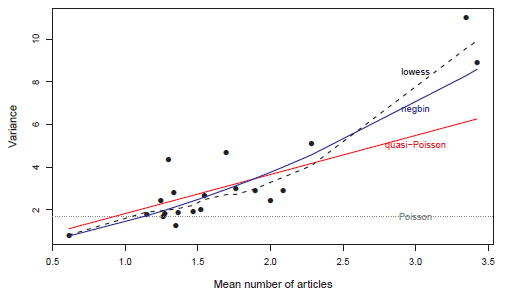
  Mean–variance functions for the PhdPubs data. Points show the observed means and variances for 20 quantile groups based on the fitted values in the negative-binomial model. The labeled lines and curves show the variance functions implied by various models.
• 

  Figure 11.10

  Hanging rootograms for the CrabSatellites data.
• 

  Figure 11.14

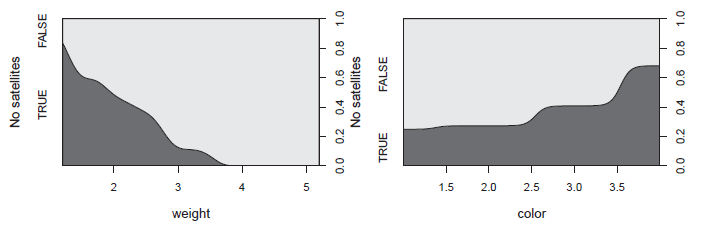
  Conditional density plots for the CrabSatellites data. The region shaded below shows the conditional probability density estimate for a count of zero.
• 

  Figure 11.17

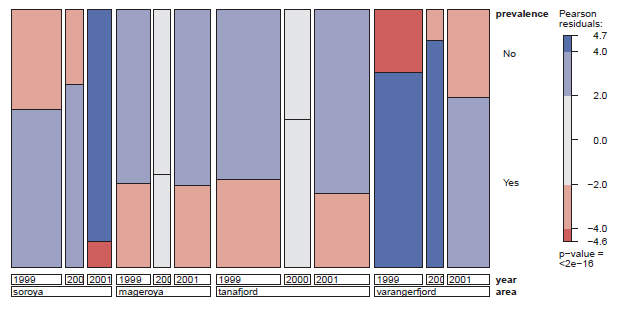
  Mosaic plot for prevalence against area and year in the CodParasites data, in the doubledecker format. Shading reflects departure from a model in which prevalence is independent of area and year jointly.
• 

  Figure 11.19

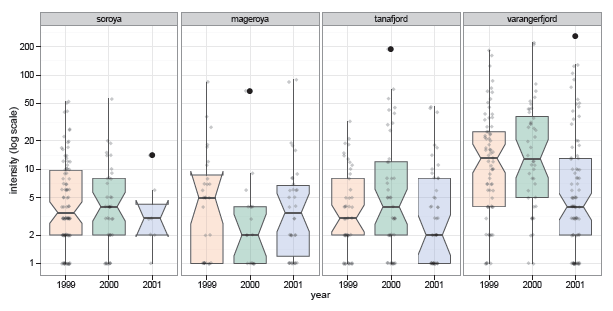
  Notched boxplots for log (intensity) of parasites by area and year in the CodParasites data. Significant differences in the medians are signaled when the notches of two groups do not overlap.
• 

  Figure 11.23

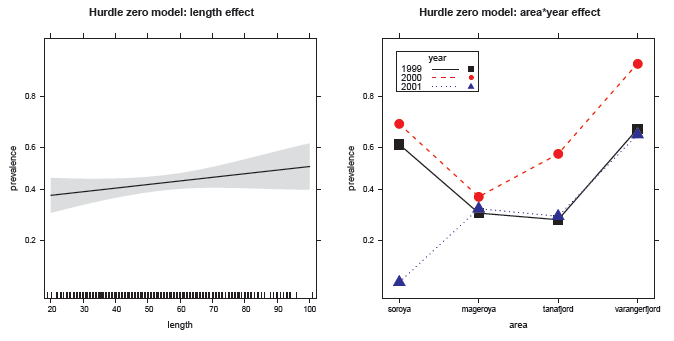
  Effect plots for prevalence of parasites analogous to the hurdle negative-binomial model, fitted using a binomial GLM model.
• 

  Figure 11.25

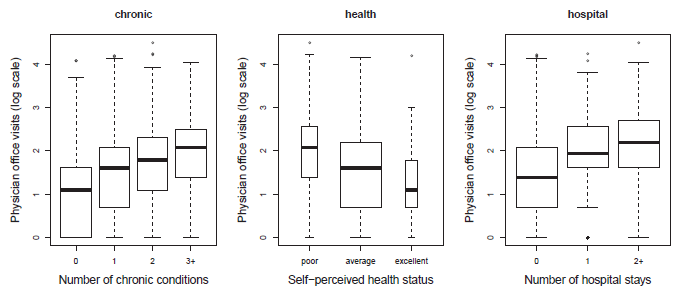
  Number of physician office visits plotted against some of the predictors.
• 

  Figure 11.27

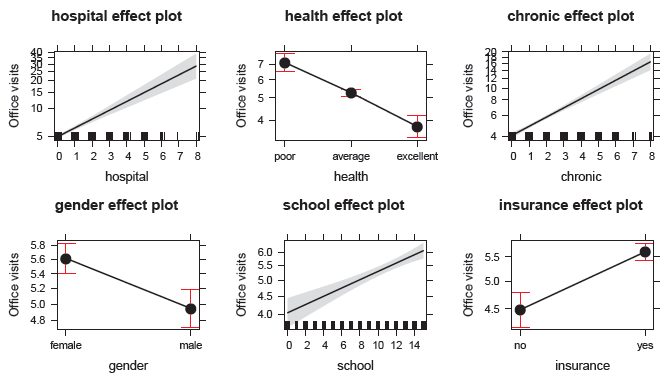
  Effect plots for the main effects of each predictor in the negative binomial model nmes.nbin.
• 

  Figure 11.30

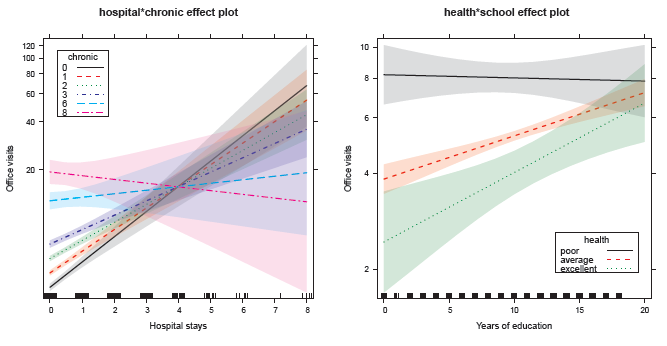
  Effect plots for the interactions of chronic conditions and hospital stays with perceived health status in the model nmes.nbin2.
• 

  Figure 11.32

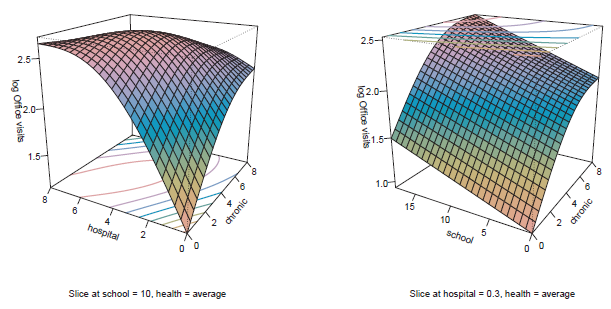
  Fitted response surfaces for the relationships among chronic conditions, number of hospital stays, and years of education to office visits in the generalized additive model, nmes.gamnb.
• 

  Figure 11.36

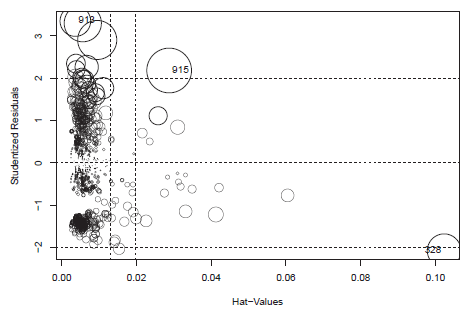
  Influence plot showing leverage, studentized residuals, and Cook’s distances for the negative-binomial model fit to the PhdPubs data. Conventional cutoffs for studentized residuals are shown by dashed horizontal lines at +/- 2; vertical lines show 2 and 3 times the average hat-value.
• 

  Figure 11.39

  Further plots of studentized residuals. Left: density plot; right: residuals against log(articles+1).
• 

  Figure 11.40

  Pairwise HE plots for all responses in the nmes2 data.
• 

  Figure 11.41

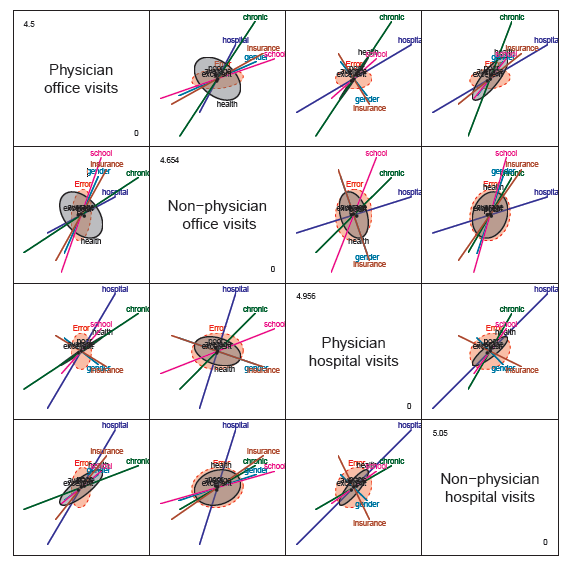
  Fourfold displays for the association between practitioner and place in the nmes.long data, conditioned on health status.
• 

  Figure 11.43

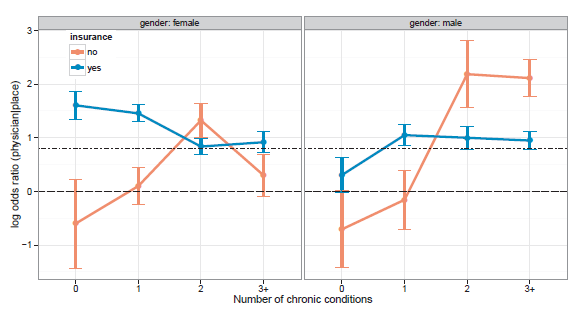
  Plot of log odds ratios with 1 standard error bars for the association between practitioner and place, conditioned on gender, insurance, and number of chronic conditions. The horizontal lines show the null model (longdash) and the mean (dot–dash) of the log odds ratios.